本文版权归作者所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
转载自夜明的孤行灯
本文链接地址: https://www.huangyunkun.com/2015/05/27/spark-gradient-descent/
梯度下降是一个最优化算法,通常也称为最速下降。
梯度下降是求解无约束优化问题最简单和最古老的方法之一,许多有效算法都是以它为基础进行改进和修正而得到的。
最速下降是用负梯度方向为搜索方向的,最速下降法越接近目标值,步长越小,前进越慢。
虽然古老而简单,但是很多时候依然可以将它用在一些情况中,也很适合快速入门。
Spark中的优化组件
Spark中的MLlib下的optimization包含了梯度下降的相关组件。
从数理基础和很多改进算法来看,梯度下降的主要抽象集中在两个方面,即如何度量梯度和如何更新参数。
Spark中的梯度抽象为Gradient.scala
abstractclass Gradient extends Serializable {
def compute(data: Vector, label: Double, weights: Vector): (Vector, Double) = {
val gradient = Vectors.zeros(weights.size)
val loss = compute(data, label, weights, gradient)
(gradient, loss)
}
def compute(data: Vector, label: Double, weights: Vector, cumGradient: Vector): Double
}
而更新抽象为Updater.scala
abstractclass Updater extends Serializable {
def compute(
weightsOld: Vector,
gradient: Vector,
stepSize: Double,
iter: Int,
regParam: Double): (Vector, Double)
}
而具体的实现梯度有
- LogisticGradient
- LeastSquaresGradient
- HingeGradient
对于更新也是三种实现
- SimpleUpdater
- L1Updater
- SquaredL2Updater
Spark本身包含了很多内置的机器学习算法,比如线性回归,分类等等,它们都有依赖梯度下降算法,所有单纯从使用角度并不需要太关心这个,因为使用的时候一般不需要具体指定。
比如线性回归:
IsotonicRegressionModel model =new IsotonicRegression().setIsotonic(true).run(training);
直接使用梯度下降
出于很多原因,大部分时候需要直接调用梯度下降,或者自己实现更新器,达到自定义的目的。
这里以简单的y=3*x+1为例来简单使用一下
测试数据就随意
1 0 1
7 2 1
10 3 1
4 1 1
19 6 1
先将它们转为RDD对象
List < Tuple2 < Object,Vector >> list = Lists.newArrayList(
new Tuple2 < >(1d, Vectors.dense(0.0d,1d)),
new Tuple2 < >(7d, Vectors.dense(2.0d,1d)),
new Tuple2 < >(10d, Vectors.dense(3.0d,1d)),
new Tuple2 < >(4d, Vectors.dense(1.0d,1d)),
new Tuple2 < >(19d, Vectors.dense(6.0d,1d))
);
JavaPairRDD < Object,Vector > rdd = jsc.parallelizePairs(list);
构造求解器
Gradient gradient =new LeastSquaresGradient();
Updater updater =new L1Updater();
Optimizer descent =new GradientDescent(gradient, updater);
调用求解
Vector optimize = descent.optimize(rdd.rdd(), Vectors.dense(0d,0d));
System.out.println(optimize);
输出如图:
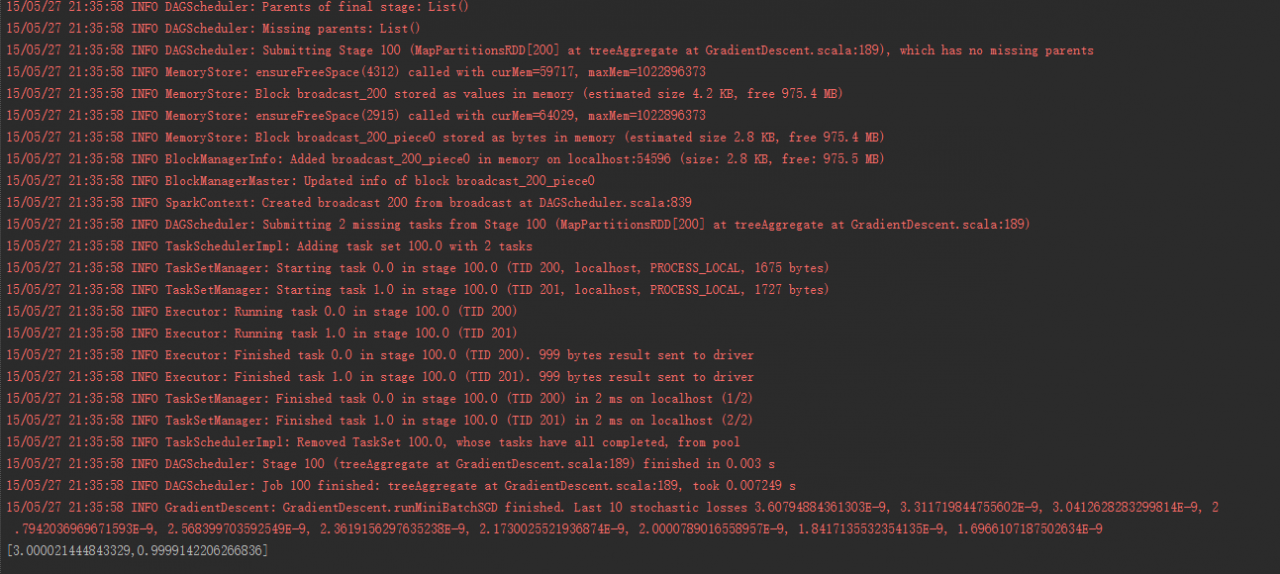
本文版权归作者所有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
转载自夜明的孤行灯
本文链接地址: https://www.huangyunkun.com/2015/05/27/spark-gradient-descent/